
The spiral of Theodorus is a spiral composed of right triangles. Hundreds of years ago, Theodorus of Cyrene constructed continuous right triangles and got a beautiful spiral. He used that spiral to prove that all non-square integers from 3–17 are irrational.
How would you plot this spiral? At each step, you need to draw a segment of length 1, perpendicular to the hypotenuse of the previous triangle. There are two perpendicular directions, and you want to choose the one that moves counterclockwise.

If we step outside the xy plane, we can compute the cross product of the unit vector in the z direction with the vector (x, y). The cross product will be perpendicular to both, and by the right-hand rule, it will point in the counterclockwise direction.
The cross product of (0, 0, 1) and (x, y, 0) is (-y, x, 0), so the direction we want to go in the xy plane is (-y, x). We divide this vector by its length to get a vector of length 1, then add it to our previous point.
Here is a code written in Python to plot the spiral
import matplotlib.pyplot as plt
def vertex(x, y):
h = (x**2 + y**2)**0.5
return (x - y/h, y + x/h)
plt.axes().set_aspect(1)
plt.axis('off')
# base of the first triangle
plt.plot([0, 1], [0, 0])
N = 17
x_old, y_old = 1, 0
for n in range(1, N):
x_new, y_new = vertex(x_old, y_old)
# draw short side
plt.plot([x_old, x_new], [y_old, y_new])
# draw hypotenuse
plt.plot([0, x_new], [0, y_new])
x_old, y_old = x_new, y_new
plt.show()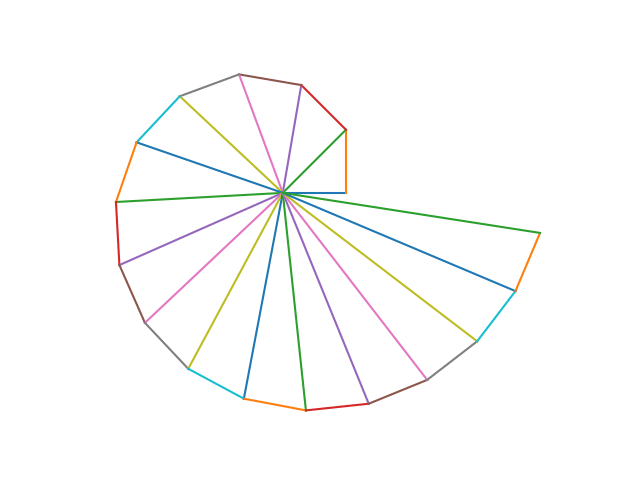
 checksum: 38957cccdef0229b17dfce1dfb41c983f71f59d88a0e338d8718d21943258cae965609e9d16032c9fa87a0271e120d2c465784b7048fa0c9cd7dfecbe94e7680
checksum: 38957cccdef0229b17dfce1dfb41c983f71f59d88a0e338d8718d21943258cae965609e9d16032c9fa87a0271e120d2c465784b7048fa0c9cd7dfecbe94e7680